Using the Gaussian Approximation
The ultimate goal of this modeling is to be able to say something about the localization of the particle in space. So far we have used eigenvectors to find the probability of finding a particle at a particular location over time, but we can also introduce a Gaussian wavepacket to better understand how position evolves with time.
The Fourier Transform
The Gaussian is a special case where there is minimum uncertainty in both position and momentum. This allows the curve to look similarly both in the position and the momentum space. The Forier transform translates a curve from one domain to its complimentary domain. In the case of the Gaussian curve in the position domain and its complimentary momentum domain, it appears with the same bell-shape curve in both domains.
This makes the Gaussian a good model. While the Gaussian model has the smallest uncertainty in both position and momentum, there is still a relationship between the shapes of the curve in these two domains. We can use this understanding of uncertainty to think about how the probability density of the position domain relates to the probability density of the momentum domain for the same state. If the curve is narrow in the position domain, that is there is a larger probability of finding the particle at a certain position, the curve of the Gaussian in the momentum domain will be broader - this is to say there is a wider distribution of possible momenta, as there is more uncertainty in the momentum. If there is greater uncertainy in the momentum (if the curve is broad in the momentum space), the curve in the position space will in turn also broaden, as the momenta which are faster would contribute to the particle moving faster to a new location and the slower momenta would contribute to the particle moving slower to a new location, increasing uncertainty in the location of the particle and causing a broadening in the Gaussian.
What does this look like over time?
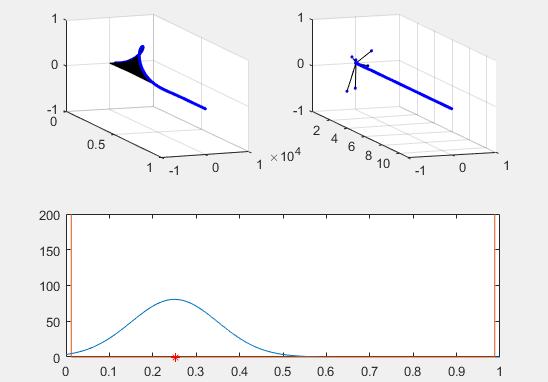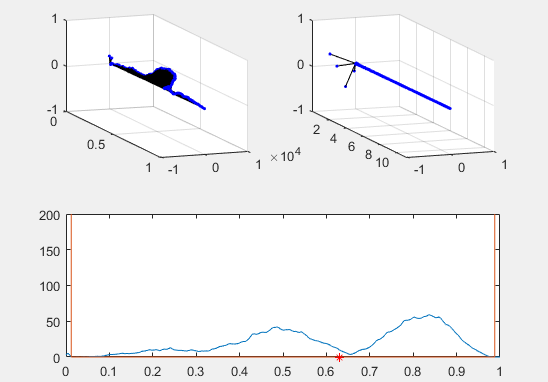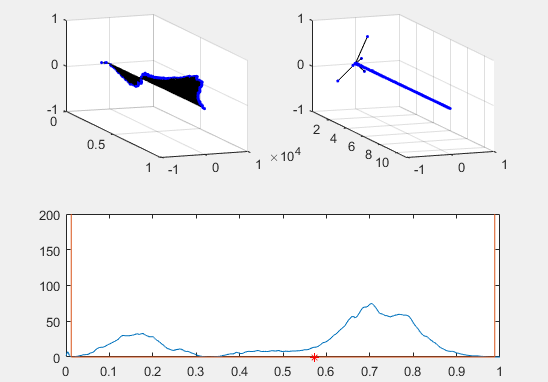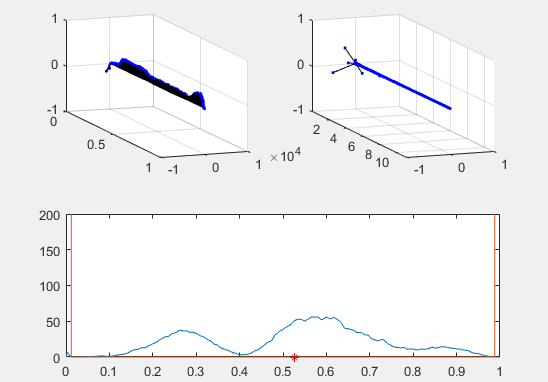
Note the red star, the expectation value of the particle fit to this Gaussian curve and how it changes over time.
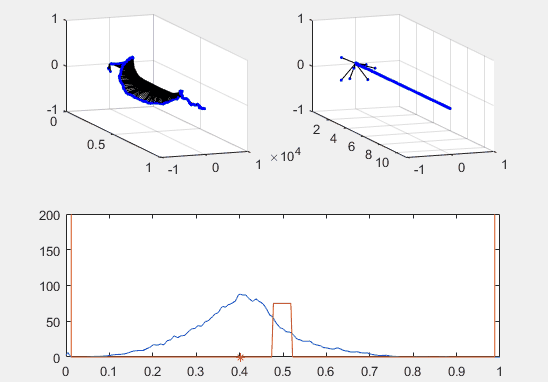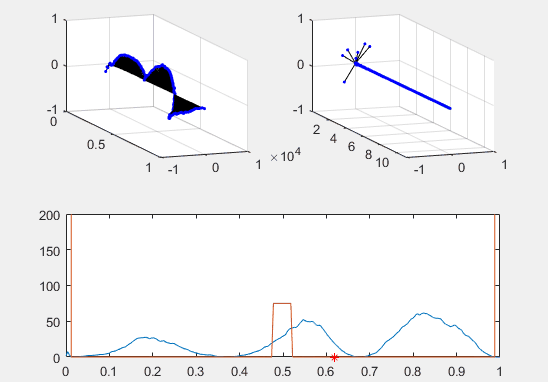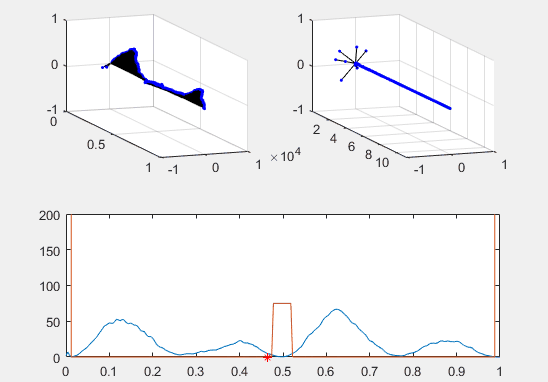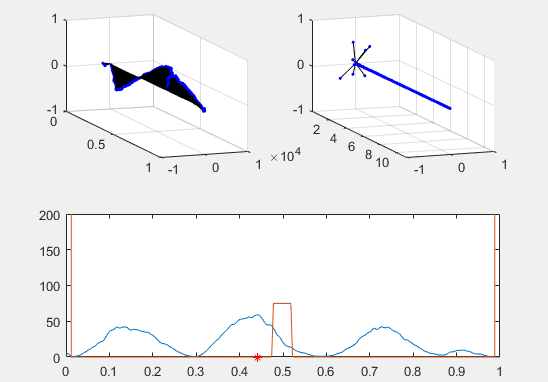
We’ve set the probability density to begin slightly to the left of the barrier, and we’ve added in a barrier to make the behavior of the particle more interesting.
The curve behaves in a less complicated fashion when the barrier is removed:
Matlab Code to Include the Gaussian
function [x,E,psiX,psiE]=TDSE
First a number of different constants must be defined. Here, the mass of the particle (m), the length of the box (L), and ${(\hbar)^2}$ are all defined as 1 in order to simplify the problem. The height of the barrier is defined as a large number to account for the infinite potential of the box and is set at ${1 x 10^6}$. A new variable w is defined as 3 in order to construct the potential wall, where w is essentially the width of the barrier. The number points used is set equal to 250.
%here are my constants: %m is mass, L is length of box, barht height of barrier, w is the barrier width
m = 1;
L = 1;
hbarsq = 1;
barht = 1e6;
w=3;
pts = 250;
The number of elements in the x vector is now defined. The linspace command is used to create a vector of x values which span from zero to the box length and are composed of pts number of elements. These x elements are evenly spaced between 0 and L. The change in x between all of these points is constant, as the points are evenly spaced and defined here as the difference between the second x element and the first x element.
%now account for the delta x and discritize the number of elements in the x vector
x = linspace(0, L, pts)';
dx = x(2)-x(1);
The potential vector ${Vvec}$ can now be constructed by creating a vector of zeros. This defines the potential energy within the box to zero, and by setting the first and last three entries of the barrier equal to the ${barht}$ defined above, a well with infinite potential is created. A barrier is also put into the middle of the box in order to determine how the behavior of the Gaussian wavepacket changes with the introduction of an additional barrier.
%x is a vector that goes from 0 to L separated by some amount, dictated by the number
%of points. Vvec is a vector with the dimension of pts entries with one column
% now we have points number of entries in the x vector
Vvec = zeros(pts, 1);
Vvec([1:w, end - (w-1):end]) = barht;
Vvec(120:130) = 75;
%this
By putting the entries of Vvec on the diagonal of a new matrix, V, the potential energy matrix has been created.
%Now we create the potential energy matrix but putting the entries of Vvec in a diagonal matrix
V = diag(Vvec);
We’ve then created a matrix which will find the kinetic energy of a different matrix. The second derivative of a function can be thought of as how the change in slope of a graph changes, and a similar thought is used here to consider how the change in entries of a vector change. This second derivative matrix shown below is then multiplied by $ {1/dx^2} $and that resulting matrix is then multiplied by $\frac{\hbar^2}{2* m}$ to determine the total kinetic energy of the vector.
```%making the second derivative matrix
D2 = (1/(dx^2))(-2eye(pts) + diag(ones(pts-1,1), 1) + diag(ones(pts-1,1),-1));
%now account for the delta x idea by subtracting the first element from the second element because they will be evenly spaced, and multiply the matrix by the constants
T = (-hbarsq/(2m))D2;
A new matrix H is then defined as the sum of the potential energy matrix and the kinetic energy matrix, as the Hamiltonian takes both the potential energy and kinetic energy in account in order to solve the total energy of a state.
%here’s our Hamiltonian, which accounts for both the potential energy and kinetic energy
H= T + V;
The [[vecs, vals]] command creates two new matrices which are the eigenvectors and eigenvalues of the matrix, H. The vecs matrix has the eigenvectors of H as columns in the matrix, and the vals matrix has all of the eigenvalues for H on the diagonal of the matrix.
%now we want to solve for the eigenvalues of the square matrix H
[vecs, vals] = eig(H);
The srtvecs commmand, [described here](/Chem-308/Eigsort.html) puts the eigenvectors and eigenvalues together in ascending order of energy level.
%now we sort the vectors and values so that they are plotted in ascending order of n, but the eigenvalues and eigenvectors stay together [srtvecs, srtvals] = eigsort(vecs, vals);
Two matrices must now be created in order to change from the position basis to the energy basis so that the wavevector may be represented in the energy basis. The idea behind the change of basis is described on the [Change of Basis page](/Chem-308/Basis.html). By multiplying the matrix EtoX by the matrix psiE, the corresponding stationary state is found in the energy basis. Here, psiX is defined by a Gaussian wavepacket and (x-0.25) term shifts the wavepacket over to the left side of the box, while the K value scales it to take up around a quarter of the box initially.
EtoX = srtvecs; XtoE = inv(srtvecs);
%now set the Gaussian to take up a quarter of the box and shift it over to the left side K=4; psiX = exp(-25((x - .25).^2)) . exp(i.K.x); psiE = XtoE*psiX;
The matrix E is now a vector composed of the diagonal elements of the srtvals matrix, which are the eigenvalues sorted in ascending order.
E = diag(srtvals);
The time evolution aspect will now be defined. The dt value determines how quickly the time evolution occurs.
t = 0; dt = 0.005;
The time evolution of this stationary state can now be visualized. The variable k defines how many points are observed during the time evolution. First the time dependence of the wavevector in the energy basis is introduced in psiEt. This new matrix can now be changed into the position basis. These vectors are also then normalized, and the concept of normalization is further developed [here](/Chem-308/Background.html).
for k = 1:100 %introduce time evolution psiEt = psiE.exp((-1iEt)/hbarsq); psiXt = EtoXpsiEt %normalize these vectors psiXt = psiXt/norm(psiXt); psiEt = psiEt/norm(psiEt);
The probability density of the normalized wavevector is then found in the position space, as the probabiltiy density is represented by the square modulus of the wavevector in position space. This probability density is then scaled in order to be better visualized.
%the probability density would be the normalized psiX * normpsiX
%complex conjugate
prob = 5000* abs(psiXt).^2; ```
Ultimately, the second energy eigenvector is plotted in position space and energy space. The probability density of the wavevector is also visualized on the figure as well.
figure(1)
subplot (2,2,1)
AW_plot3 (x, 5.*psiXt,1)
subplot (2,2,2)
AW_plot3 (E, psiEt,10)
subplot (2,2,[3 4])
plot(x, prob, x, Vvec)
axis([-inf inf 0 100])
The expectation value for position are then determined by finding the inner product of the position operator acting on the wavevector and the complex conjugate of the wavevector. The energy expectation value is calculated in a similar fashion as well.
% expectation value for position, plotted with a red *
xexp = real(psiXt'*(x.*psiXt));
hold on
plot (real(xexp), 0, 'r*')
% energy expectation value in energy basis
Eexp=real(psiEt'*(srtvals*psiEt));
plot (xexp, Eexp, 'b*')
text(0.2,Eexp,['E= ' num2str(Eexp)])
hold off
drawnow
t = t + dt;
end
end